title: javascript 数据结构与算法–学习笔记
date: 2016-03-20 14:11:30
tags: [笔记, note]
—# 1.栈

对栈的理解是，栈是一段存储空间，供系统或者操作系统使用，对程序员来说一般是不可见的，除非从一开始由程序员自己通过汇编等自己构建栈，栈会由系统管理单元自己申请释放。栈是从高地址向低地址生长的，既栈底在高地址，栈顶低地址。

2.堆

通俗意义上这样理解堆，堆是一段非常大的内存空间，供不同的程序员从其中取出一段供自己使用，使用之后要由程序员自己释放，如果不释放的话，这部分存储空间将不能被其他程序使用。堆的存储空间是不连续的，因为会因为不同时间，不同大小的堆空间的申请导致其不连续性。堆的生长是从低地址向高地址增长的。

3.基本算法

3.1 冒泡算法：

1
2
3
4
5
6
7
8
9
10
11
var arr = [2, 1, 4, 3];
for (var i = 0; i < arr.length; i++) {
  for (var j = 0; j < arr.length; j++) {
		if(arr[i]>arr[j]){
    	var x = arr[j];				//重点就是这个中间值做转换
      arr[j] = arr[i];
      arr[i] = x;
    }
  }
}
console.log(arr)

3.2 快排算法:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
    var arr = [7, 5, 7, 2, 1, 6, 9, 7, 5, 6];
    var i = 0,
            j = arr.length - 1;
    function sort(arr) {

        var bridge = arr[i];
        if (arr[i] >= arr[j]) {
            arr[i] = arr[j];
            arr[j] = bridge;
            j--;
            if (j > i) {
                sort(arr);
            } else {
                i++;
                if(i<=arr.length-2){
                    j = arr.length - 1;
                    sort(arr);
                }else{
                    return arr;
                }

            }
        } else {
            j--;
            if (j > i) {
                sort(arr);
            }else{
                i++;
                if(i<=arr.length-2){
                    j = arr.length - 1;
                    sort(arr);
                }else{
                    return arr;
                }
            }
        }
        return arr;
    }


//    ★简化后

//    function sort(arr) {
//        var bridge = arr[i];
//        if (arr[i] >= arr[j]) {
//            arr[i] = arr[j];
//            arr[j] = bridge;
//        }
//        j--;
//        if (j > i) {
//            sort(arr);
//        } else {
//            i++;
//            if (i <= arr.length - 2) {
//                j = arr.length - 1;
//                sort(arr);
//            }
//        }
//        return arr;
//    }

    var newArr = sort(arr);
    console.log(newArr)

1.javascript 简介

1.2.4 相等操作符

toPrimitive 方法是内部方法，对不同类型返回的结果是，如果对象的 valueOf 方法的结果是原始值，返回原始值。如果对象的 toString 方法返回原始值，就返回这个值，其他情况返回一个错误

1.3.1 条件语句

对于 switch 语句来说，case和break关键字非常重要。

1.4 函数

函数只接受一个参数的话，如果传入两个参数，会忽略掉第二个参数。

1.5 面向对象编程

原型方法：可以节约内存和降低实例化的开销
私有方法：用在类定义内部声明的方式

2. 数组

数组缺点：（在大多数语言中）数组的大小是固定的，从数组的起点或中间插入或移除项的成本很高，因为需要移动元素

2.4 二维和多维数组

嵌套循环

1
arr = [[],[]]

2.5.3 搜索和排序

sort方法对数组做排序，是把元素默认成字符串对应的 ASCII 值进行比较的
如果有重音符号的排序，可以用 localCompare 来实现（原理好像是通过 Unicode 编码来排序的）

3. 栈

遵从后进先出(LIFO)原则的有序集合。
栈的方法
 push(element(s)) ：添加一个（或几个）新元素到栈顶。
 pop() ：移除栈顶的元素，同时返回被移除的元素。
 peek() ：返回栈顶的元素，不对栈做任何修改（这个方法不会移除栈顶的元素，仅仅返回它） 。
 isEmpty() ：如果栈里没有任何元素就返回 true ，否则返回 false 。
 clear() ：移除栈里的所有元素。
 size() ：返回栈里的元素个数。这个方法和数组的 length 属性很类似。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
function Stack() {
    var items = [];
    this.push = function(element){
        items.push(element);
    };
    this.pop = function(){
        return items.pop();
    };
    this.peek = function(){
        return items[items.length-1];
    };
    this.isEmpty = function(){
        return items.length == 0;
    };
    this.size = function(){
        return items.length;
    };
    this.clear = function(){
        items = [];
    };
    this.print = function(){
        console.log(items.toString());
    };
    this.toString = function(){
        return items.toString();
    };
}

3.2 十进制转二进制

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
function divideBy2(decNumber){

    var remStack = new Stack(),
        rem,
        binaryString = '';

    while (decNumber > 0){
        rem = Math.floor(decNumber % 2);
        remStack.push(rem);
        decNumber = Math.floor(decNumber / 2);
    }

    while (!remStack.isEmpty()){
        binaryString += remStack.pop().toString();
    }

    return binaryString;
}

console.log(divideBy2(233));
console.log(divideBy2(10));
console.log(divideBy2(1000));

4. 队列

遵从（FIFO）先进先出原则的一组有序的项。
队列的方法：
 enqueue(element(s)) ：向队列尾部添加一个（或多个）新的项。
 dequeue() ：移除队列的第一（即排在队列最前面的）项，并返回被移除的元素。
 front() ：返回队列中第一个元素——最先被添加，也将是最先被移除的元素。队列不做任何变动（不移除元素，只返回元素信息——与 Stack 类的 peek 方法非常类似） 。
 isEmpty() ：如果队列中不包含任何元素，返回 true ，否则返回 false 。
 size() ：返回队列包含的元素个数，与数组的 length 属性类似。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
function Queue() {
    var items = [];
    this.enqueue = function(element){
        items.push(element);
    };
    this.dequeue = function(){
        return items.shift();
    };
    this.front = function(){
        return items[0];
    };
    this.isEmpty = function(){
        return items.length == 0;
    };
    this.clear = function(){
        items = [];
    };
    this.size = function(){
        return items.length;
    };
    this.print = function(){
        console.log(items.toString());
    };
}

4.2 优先队列

例子：急诊科，医生会根据病情优先病情严重的人先看

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
function PriorityQueue() {
    var items = [];
    function QueueElement (element, priority){
        this.element = element;
        this.priority = priority;
    }
    this.enqueue = function(element, priority){
        var queueElement = new QueueElement(element, priority);
        if (this.isEmpty()){
            items.push(queueElement);
        } else {
            var added = false;
            for (var i=0; i<items.length; i++){
                if (queueElement.priority < items[i].priority){
                    items.splice(i,0,queueElement);   //数组的插入方法
                    added = true;
                    break;
                }
            }
            if (!added){
                items.push(queueElement);
            }
        }
    };

    this.dequeue = function(){
        return items.shift();
    };
    this.front = function(){
        return items[0];
    };
    this.isEmpty = function(){
        return items.length == 0;
    };
    this.size = function(){
        return items.length;
    };
    this. print = function(){
        for (var i=0; i<items.length; i++){
            console.log(items[i].element + ' - ' + items[i].priority);
        }
    };
}

var priorityQueue = new PriorityQueue();
priorityQueue.enqueue("John", 2);
priorityQueue.enqueue("Jack", 1);
priorityQueue.enqueue("Camila", 1);
priorityQueue.enqueue("Maxwell", 2);
priorityQueue.enqueue("Ana", 3);
priorityQueue.print();

4.3 循环列队–击鼓传花

某一时刻传花停止，这个时候花在谁手里，谁就退出圆圈结束游戏。重复这个过程，直到只剩一个孩子（胜者） 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function hotPotato (nameList, num){
 var queue = new Queue();
 for (var i=0; i<nameList.length; i++){
     queue.enqueue(nameList[i]);
 }
 var eliminated = '';
 while (queue.size() > 1){
     for (var i=0; i<num; i++){
         queue.enqueue(queue.dequeue());        //循环起来，传num次
     }
     eliminated = queue.dequeue();  //传了num后的最后一个人就是被淘汰的人
     console.log(eliminated + ' was eliminated from the Hot Potato game.');
 }
 return queue.dequeue();
}

var names = ['John','Jack','Camila','Ingrid','Carl'];
var winner = hotPotato(names, 7);
console.log('The winner is: ' + winner);

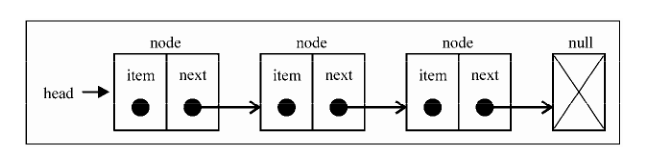
5. 链表

数组缺点：（在大多数语言中）数组的大小是固定的，从数组的起点或中间插入或移除项的成本很高，因为需要移动元素
链表：存储有序的元素集合，但不同于数组，链表中的元素在内存中并不是连续放置的。每个元素由一个存储元素本身的节点和一个指向下一个元素的引用（也称指针或链接）组成。

链表缺点：数组的另一个细节是可以直接访问任何位置的任何元素，而要想访问链表中间的一个元素，需要从起点（表头）开始迭代列表直到找到所需的元素。

链表方法：
 append(element) ：向列表尾部添加一个新的项。
 insert(position, element) ：向列表的特定位置插入一个新的项。
 remove(element) ：从列表中移除一项。
 indexOf(element) ：返回元素在列表中的索引。如果列表中没有该元素则返回 -1 。
 removeAt(position) ：从列表的特定位置移除一项。
 isEmpty() ： 如果链表中不包含任何元素， 返回 true ， 如果链表长度大于 0 则返回 false 。
 size() ：返回链表包含的元素个数。与数组的 length 属性类似。
 toString() ：由于列表项使用了 Node 类，就需要重写继承自 JavaScript 对象默认的 toString 方法，让其只输出元素的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
//current 是不存在的会被node替换掉
function LinkedList() {
    var Node = function(element){

        this.element = element;
        this.next = null;
    };
    var length = 0;
    var head = null;
    this.append = function(element){
        var node = new Node(element),
            current;
        if (head === null){ //first node on list
            head = node;
        } else {
            current = head;
            //loop the list until find last item
            while(current.next){
                current = current.next;
            }
            //get last item and assign next to added item to make the link
            current.next = node;
        }
        length++; //update size of list
    };
    this.insert = function(position, element){
        //check for out-of-bounds values
        if (position >= 0 && position <= length){
            var node = new Node(element),
                current = head,
                previous,
                index = 0;
            if (position === 0){ //add on first position
                node.next = current;
                head = node;
            } else {
                while (index++ < position){
                    previous = current;
                    current = current.next;
                }
                node.next = current;
                previous.next = node;
            }
            length++; //update size of list
            return true;
        } else {
            return false;
        }
    };
    this.removeAt = function(position){
        //check for out-of-bounds values
        if (position > -1 && position < length){
            var current = head,
                previous,
                index = 0;
            //removing first item
            if (position === 0){
                head = current.next;
            } else {
                while (index++ < position){
                    previous = current;
                    current = current.next;
                }
                //link previous with current's next - skip it to remove
                previous.next = current.next;
            }
            length--;
            return current.element;
        } else {
            return null;
        }
    };
    this.remove = function(element){
        var index = this.indexOf(element);
        return this.removeAt(index);
    };
    this.indexOf = function(element){
        var current = head,
            index = 0;
        while (current) {
            if (element === current.element) {
                return index;
            }
            index++;
            current = current.next;
        }
        return -1;
    };
    this.isEmpty = function() {
        return length === 0;
    };
    this.size = function() {
        return length;
    };
    this.getHead = function(){
        return head;
    };
    this.toString = function(){
        var current = head,
            string = '';
        while (current) {
            string = current.element;
            current = current.next;
        }
        return string;
    };
    this.print = function(){
        console.log(this.toString());
    };
}

5.2 双向链表

在单向链表中，如果迭代列表时错过了要找的元素，就需要回到列表起点，重新开始迭代。这是双向链表的一个优点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
function DoublyLinkedList() {
    var Node = function(element){
        this.element = element;
        this.next = null;
        this.prev = null; //NEW
    };
    var length = 0;
    var head = null;
    var tail = null; //NEW
    this.append = function(element){
        var node = new Node(element),
            current;
        if (head === null){ //first node on list
            head = node;
            tail = node; //NEW
        } else {
            //attach to the tail node //NEW
            tail.next = node;
            node.prev = tail;
            tail = node;
        }
        length++; //update size of list
    };
    this.insert = function(position, element){
        //check for out-of-bounds values
        if (position >= 0 && position <= length){
            var node = new Node(element),
                current = head,
                previous,
                index = 0;
            if (position === 0){ //add on first position
                if (!head){       //NEW
                    head = node;
                    tail = node;
                } else {
                    node.next = current;
                    current.prev = node; //NEW {1}
                    head = node;
                }
            } else  if (position === length) { //last item //NEW
                current = tail;     // {2}
                current.next = node;
                node.prev = current;
                tail = node;
            } else {
                while (index++ < position){ //{3}
                    previous = current;
                    current = current.next;
                }
                node.next = current;
                previous.next = node;
                current.prev = node; //NEW
                node.prev = previous; //NEW
            }
            length++; //update size of list
            return true;
        } else {
            return false;
        }
    };
    this.removeAt = function(position){
        //check for out-of-bounds values
        if (position > -1 && position < length){
            var current = head,
                previous,
                index = 0;
            //removing first item
            if (position === 0){
                head = current.next; // {1}
                //if there is only one item, then we update tail as well //NEW
                if (length === 1){ // {2}
                    tail = null;
                } else {
                    head.prev = null; // {3}
                }
            } else if (position === length-1){ //last item //NEW
                current = tail; // {4}
                tail = current.prev;
                tail.next = null;
            } else {
                while (index++ < position){ // {5}
                    previous = current;
                    current = current.next;
                }
                //link previous with current's next - skip it to remove
                previous.next = current.next; // {6}
                current.next.prev = previous; //NEW
            }
            length--;
            return current.element;
        } else {
            return null;
        }
    };
    this.remove = function(element){
        var index = this.indexOf(element);
        return this.removeAt(index);
    };
    this.indexOf = function(element){
        var current = head,
            index = -1;
        //check first item
        if (element == current.element){
            return 0;
        }
        index++;
        //check in the middle of the list
        while(current.next){
            if (element == current.element){
                return index;
            }
            current = current.next;
            index++;
        }
        //check last item
        if (element == current.element){
            return index;
        }
        return -1;
    };
    this.isEmpty = function() {
        return length === 0;
    };
    this. size = function() {
        return length;
    };
    this.toString = function(){
        var current = head,
            s = current ? current.element : '';
        while(current && current.next){
            current = current.next;
            s += ', ' + current.element;
        }
        return s;
    };
    this.inverseToString = function() {
        var current = tail,
            s = current ? current.element : '';
        while(current && current.prev){
            current = current.prev;
            s += ', ' + current.element;
        }
        return s;
    };
    this.print = function(){
        console.log(this.toString());
    };
    this.printInverse = function(){
        console.log(this.inverseToString());
    };
    this.getHead = function(){
        return head;
    };
    this.getTail = function(){
        return tail;
    }
}

5.3 循环列表

6. 集合（Set 类） [值，值]–其实就是 key=value

集合：由一组无序且唯一（即不重复）的项组成的。
方法有：
 add(value) ：向集合添加一个新的项。
 remove(value) ：从集合移除一个值。
 has(value) ：如果值在集合中，返回 true ，否则返回 false 。
 clear() ：移除集合中的所有项。
 size() ：返回集合所包含元素的数量。与数组的 length 属性类似。
 values() ：返回一个包含集合中所有值的数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
function Set() {

    var items = {};

    this.add = function(value){
        if (!this.has(value)){
            items[value] = value;
            return true;
        }
        return false;
    };

    this.remove = function(value){
        if (this.has(value)){
            delete items[value];
            return true;
        }
        return false;
    };

    this.has = function(value){
        return items.hasOwnProperty(value);
        //return value in items;
    };

    this.clear = function(){
        items = {};
    };

    /**
     * Modern browsers function
     * IE9+, FF4+, Chrome5+, Opera12+, Safari5+
     * @returns {Number}
     */
    this.size = function(){
        return Object.keys(items).length;
    };

    /**
     * cross browser compatibility - legacy browsers
     * for modern browsers use size function
     * @returns {number}
     */
    this.sizeLegacy = function(){
        var count = 0;
        for(var prop in items) {
            if(items.hasOwnProperty(prop))
                ++count;
        }
        return count;
    };

    /**
     * Modern browsers function
     * IE9+, FF4+, Chrome5+, Opera12+, Safari5+
     * @returns {Array}
     */
    this.values = function(){
        return Object.keys(items);
    };

    this.valuesLegacy = function(){
        var keys = [];
        for(var key in items){
            keys.push(key);
        }
        return keys;
    };

    this.getItems = function(){
      return items;
    };

    this.union = function(otherSet){
        var unionSet = new Set(); //{1}

        var values = this.values(); //{2}
        for (var i=0; i<values.length; i++){
            unionSet.add(values[i]);
        }

        values = otherSet.values(); //{3}
        for (var i=0; i<values.length; i++){
            unionSet.add(values[i]);
        }

        return unionSet;
    };

    this.intersection = function(otherSet){
        var intersectionSet = new Set(); //{1}

        var values = this.values();
        for (var i=0; i<values.length; i++){ //{2}
            if (otherSet.has(values[i])){    //{3}
                intersectionSet.add(values[i]); //{4}
            }
        }

        return intersectionSet;
    };

    this.difference = function(otherSet){
        var differenceSet = new Set(); //{1}

        var values = this.values();
        for (var i=0; i<values.length; i++){ //{2}
            if (!otherSet.has(values[i])){    //{3}
                differenceSet.add(values[i]); //{4}
            }
        }

        return differenceSet;
    };

    this.subset = function(otherSet){

        if (this.size() > otherSet.size()){ //{1}
            return false;
        } else {
            var values = this.values();
            for (var i=0; i<values.length; i++){ //{2}
                if (!otherSet.has(values[i])){    //{3}
                    return false; //{4}
                }
            }
            return true;
        }
    };
}

7. 字典（Map） [键，值] 和 散列表[{},{}]

字典也称映射。
字典的方法
 set(key,value) ：向字典中添加新元素。
 remove(key) ：通过使用键值来从字典中移除键值对应的数据值。
 has(key) ：如果某个键值存在于这个字典中，则返回 true ，反之则返回 false 。
 get(key) ：通过键值查找特定的数值并返回。
 clear() ：将这个字典中的所有元素全部删除。
 size() ：返回字典所包含元素的数量。与数组的 length 属性类似。
 keys() ：将字典所包含的所有键名以数组形式返回。
 values() ：将字典所包含的所有数值以数组形式返回。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
function Dictionary(){

    var items = {};

    this.set = function(key, value){
        items[key] = value; //{1}
    };

    this.remove = function(key){
        if (this.has(key)){
            delete items[key];
            return true;
        }
        return false;
    };

    this.has = function(key){
        return items.hasOwnProperty(key);
        //return value in items;
    };

    this.get = function(key) {
        return this.has(key) ? items[key] : undefined;
    };

    this.clear = function(){
        items = {};
    };

    this.size = function(){
        return Object.keys(items).length;
    };

    this.keys = function(){
        return Object.keys(items);
    };

    this.values = function(){
        var values = [];
        for (var k in items) {
            if (this.has(k)) {
                values.push(items[k]);
            }
        }
        return values;
    };

    this.each = function(fn) {
        for (var k in items) {
            if (this.has(k)) {
                fn(k, items[k]);
            }
        }
    };

    this.getItems = function(){
        return items;
    }
}

7.2 散列表–也叫 HashTable 或 HashMap

前边的数据结构在获取值的时候，需要遍历整个数据结构来找到它。如果使用散列函数，就知道值的具体位置，因此能够快速检索到该值。
散列表方法：
 put(key,value) ：向散列表增加一个新的项（也能更新散列表） 。
 remove(key) ：根据键值从散列表中移除值。
 get(key) ：返回根据键值检索到的特定的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
function HashTable() {

    var table = [];

    var loseloseHashCode = function (key) {
        var hash = 0;
        for (var i = 0; i < key.length; i++) {
            hash += key.charCodeAt(i);
        }
        return hash % 37;
    };

    var djb2HashCode = function (key) {
        var hash = 5381;
        for (var i = 0; i < key.length; i++) {
            hash = hash * 33 + key.charCodeAt(i);
        }
        return hash % 1013;
    };

    var hashCode = function (key) {
        return loseloseHashCode(key);
    };

    this.put = function (key, value) {
        var position = hashCode(key);
        console.log(position + ' - ' + key);
        table[position] = value;
    };

    this.get = function (key) {
        return table[hashCode(key)];
    };

    this.remove = function(key){
        table[hashCode(key)] = undefined;
    };

    this.print = function () {
        for (var i = 0; i < table.length; ++i) {
            if (table[i] !== undefined) {
                console.log(i + ": " + table[i]);
            }
        }
    };
}

7.2.3 散列表和散列集合

散列表：[{},{}]
散列集合： 不同之处：只插入值而没有键。只存储唯一不重复的值

7.2.4 处理散列表中的冲突

如果发生冲突：后添加的会覆盖之前添加的值

7.2.4.1 分离链接

结构为：[{key:[这里是发生冲突的项]},{key:[这里是发生冲突的项]}]
补充：[]内的结构是一个链的数据结构，不是数组的数据结构
重写方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
function HashTableSeparateChaining(){

    var table = [];

    var ValuePair = function(key, value){
        this.key = key;
        this.value = value;

        this.toString = function() {
            return '[' + this.key + ' - ' + this.value + ']';
        }
    };

    var loseloseHashCode = function (key) {
        var hash = 0;
        for (var i = 0; i < key.length; i++) {
            hash += key.charCodeAt(i);
        }
        return hash % 37;
    };

    var hashCode = function(key){
        return loseloseHashCode(key);
    };

    this.put = function(key, value){
        var position = hashCode(key);
        console.log(position + ' - ' + key);

        if (table[position] == undefined) {
            table[position] = new LinkedList();
        }
        table[position].append(new ValuePair(key, value));
    };

    this.get = function(key) {
        var position = hashCode(key);

        if (table[position] !== undefined  && !table[position].isEmpty()){

            //iterate linked list to find key/value
            var current = table[position].getHead();

            while(current.next){
                if (current.element.key === key){
                    return current.element.value;
                }
                current = current.next;
            }

            //check in case first or last element
            if (current.element.key === key){
                return current.element.value;
            }
        }
        return undefined;
    };

    this.remove = function(key){

        var position = hashCode(key);

        if (table[position] !== undefined){

            //iterate linked list to find key/value
            var current = table[position].getHead();

            while(current.next){
                if (current.element.key === key){
                    table[position].remove(current.element);
                    if (table[position].isEmpty()){
                        table[position] = undefined;
                    }
                    return true;
                }
                current = current.next;
            }

            //check in case first or last element
            if (current.element.key === key){
                table[position].remove(current.element);
                if (table[position].isEmpty()){
                    table[position] = undefined;
                }
                return true;
            }
        }

        return false;
    };

    this.print = function() {
        for (var i = 0; i < table.length; ++i) {
            if (table[i] !== undefined) {
               console.log(table[i].toString());
            }
        }
    };
}

7.2.4.2 线性探查

其实就是通过移位的方法。
定义：当想向表中某个位置加入一个新元素的时候，如果索引为 index 的位置已经被占据了，就尝试 index+1 的位置。如果 index+1 的位置也被占据了，就尝试 index+2 的位置，以此类推。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
function HashLinearProbing(){

    var table = [];

    var ValuePair = function(key, value){
        this.key = key;
        this.value = value;

        this.toString = function() {
            return '[' + this.key + ' - ' + this.value + ']';
        }
    };

    var loseloseHashCode = function (key) {
        var hash = 0;
        for (var i = 0; i < key.length; i++) {
            hash += key.charCodeAt(i);
        }
        return hash % 37;
    };

    var hashCode = function(key){
        return loseloseHashCode(key);
    };

    this.put = function(key, value){
        var position = hashCode(key);
        console.log(position + ' - ' + key);

        if (table[position] == undefined) {
            table[position] = new ValuePair(key, value);
        } else {
            var index = ++position;
            while (table[index] != undefined){
                index++;
            }
            table[index] = new ValuePair(key, value);
        }
    };

    this.get = function(key) {
        var position = hashCode(key);

        if (table[position] !== undefined){
            if (table[position].key === key) {
                return table[position].value;
            } else {
                var index = ++position;
                while (table[index] === undefined || table[index].key !== key){
                    index++;
                }
                if (table[index].key === key) {
                    return table[index].value;
                }
            }
        }
        return undefined;
    };

    this.remove = function(key){
        var position = hashCode(key);

        if (table[position] !== undefined){
            if (table[position].key === key) {
                table[position] = undefined;
            } else {
                var index = ++position;
                while (table[index] === undefined || table[index].key !== key){
                    index++;
                }
                if (table[index].key === key) {
                    table[index] = undefined;
                }
            }
        }
    };

    this.print = function() {
        for (var i = 0; i < table.length; ++i) {
            if (table[i] !== undefined) {
                console.log(i + ' -> ' + table[i].toString());
            }
        }
    };
}

7.2.5 创建更好的散列函数

之前的散列函数造成的冲突太多了。
下面这个散列函数：插入和检索元素的时间（即性能）变短，冲突可能性大大降低。

1
2
3
4
5
6
7
var djb2HashCode = function (key) {
    var hash = 5381; //{1}
    for (var i = 0; i < key.length; i++) { //{2}
        hash = hash * 33 + key.charCodeAt(i); //{3}
    }
    return hash % 1013; //{4}
};

8. 树

非顺序数据结构，对于存储需要快速查找数据非常有用
内部节点：至少有一个子节点的节点称为内部节点。
外部节点：没有子元素的节点称为外部节点或叶节点。
子树：子树由节点和它的后代构成。
深度：取决于它的祖先节点的数量。
高度：取决于所有节点深度的最大值。
边：和链表一样，将通过指针来表示节点之间的关系
键：键是树相关的术语中对节点的称呼

8.2 二叉树和二叉搜索树

二叉搜索树（BST）：左侧节点存储小的值，在右侧节点存储大（或者等于）的值。

方法：
 insert(key) ：向树中插入一个新的键。
 search(key) ：在树中查找一个键，如果节点存在，则返回 true ；如果不存在，则返回 false 。
 inOrderTraverse ：通过中序遍历方式遍历所有节点。
 preOrderTraverse ：通过先序遍历方式遍历所有节点。
 postOrderTraverse ：通过后序遍历方式遍历所有节点。
 min ：返回树中最小的值/键。
 max ：返回树中最大的值/键。
 remove(key) ：从树中移除某个键。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
function BinarySearchTree() {

    var Node = function(key){
        this.key = key;
        this.left = null;
        this.right = null;
    };

    var root = null;

    this.insert = function(key){

        var newNode = new Node(key);

        //special case - first element
        if (root === null){
            root = newNode;
        } else {
            insertNode(root,newNode);
        }
    };

    var insertNode = function(node, newNode){
        if (newNode.key < node.key){
            if (node.left === null){
                node.left = newNode;
            } else {
                insertNode(node.left, newNode);
            }
        } else {
            if (node.right === null){
                node.right = newNode;
            } else {
                insertNode(node.right, newNode);
            }
        }
    };

    this.getRoot = function(){
        return root;
    };

    this.search = function(key){

        return searchNode(root, key);
    };

    var searchNode = function(node, key){

        if (node === null){
            return false;
        }

        if (key < node.key){
            return searchNode(node.left, key);

        } else if (key > node.key){
            return searchNode(node.right, key);

        } else { //element is equal to node.item
            return true;
        }
    };
//中序遍历
    this.inOrderTraverse = function(callback){
        inOrderTraverseNode(root, callback);
    };

    var inOrderTraverseNode = function (node, callback) {
        if (node !== null) {        //停止递归继续执行的条件
            inOrderTraverseNode(node.left, callback);
            callback(node.key);
            inOrderTraverseNode(node.right, callback);
        }
    };
//先序遍历
    this.preOrderTraverse = function(callback){
        preOrderTraverseNode(root, callback);
    };

    var preOrderTraverseNode = function (node, callback) {
        if (node !== null) {
            callback(node.key);
            preOrderTraverseNode(node.left, callback);
            preOrderTraverseNode(node.right, callback);
        }
    };
//后续遍历
    this.postOrderTraverse = function(callback){
        postOrderTraverseNode(root, callback);
    };

    var postOrderTraverseNode = function (node, callback) {
        if (node !== null) {
            postOrderTraverseNode(node.left, callback);
            postOrderTraverseNode(node.right, callback);
            callback(node.key);
        }
    };

    this.min = function() {
        return minNode(root);
    };

    var minNode = function (node) {
        if (node){
            while (node && node.left !== null) {
                node = node.left;
            }

            return node.key;
        }
        return null;
    };

    this.max = function() {
        return maxNode(root);
    };

    var maxNode = function (node) {
        if (node){
            while (node && node.right !== null) {
                node = node.right;
            }

            return node.key;
        }
        return null;
    };

    this.remove = function(element){
        root = removeNode(root, element);
    };

    var findMinNode = function(node){
        while (node && node.left !== null) {
            node = node.left;
        }

        return node;
    };

    var removeNode = function(node, element){

        if (node === null){
            return null;
        }

        if (element < node.key){
            node.left = removeNode(node.left, element);
            return node;

        } else if (element > node.key){
            node.right = removeNode(node.right, element);
            return node;

        } else { //element is equal to node.item

            //handle 3 special conditions
            //1 - a leaf node
            //2 - a node with only 1 child
            //3 - a node with 2 children

            //case 1
            if (node.left === null && node.right === null){
                node = null;
                return node;
            }

            //case 2
            if (node.left === null){
                node = node.right;
                return node;

            } else if (node.right === null){
                node = node.left;
                return node;
            }

            //case 3
            var aux = findMinNode(node.right);
            node.key = aux.key;
            node.right = removeNode(node.right, aux.key);
            return node;
        }
    };
}

8.3 树的遍历

8.3.1 中序遍历

从最小到最大的顺序访问所有节点。

8.3.2 先序遍历

先序遍历是以优先于后代节点的顺序访问每个节点的。

8.3.3 后续遍历

后序遍历则是先访问节点的后代节点，再访问节点本身。

8.4 搜索树中的值

8.4.1 搜索最小值和最大值

最左边是最小值
最右边是最大值

8.4.2 搜索一个特定的值

当key<node.key 和key>node.key都不成立的时候，就是等于了！！

8.4.3 移除一个节点

当找到 node.key 的时候还有三种情况 1.无子叶 2.只有右子节点 3.只有左子节点 4.有两个子节点–需要找到右子叶最小的节点，将这个节点提到删除的那个节点去，并删除这个节点。

8.5 更多关于二叉树的知识

平衡二叉树搜索树（AVL）：因为上边讨论的方法存在一条边非常深的情况，所以通过平衡二叉树来设置左右两侧子树的高度之差最多为 1.
红黑树：这种树可以进行高效的中序遍历。

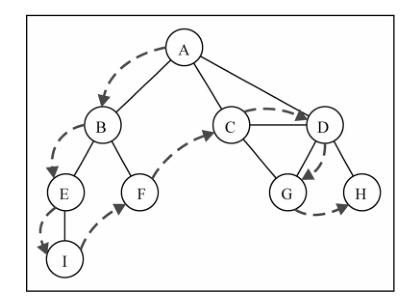
9. 图

图–非线性数据结构

9.1 图的相关术语

边(E)：
节点/顶点(V)：
度：一个顶点的度是其相邻顶点的数量。
简单路径：不包含重复的顶点
环：也是一个简单路径，比如 A D C A（最后一个顶点重新回到 A）
无环图：图中不存在环
连通图：每两个顶点间都存在路径
有向图和无向图
强连通：两个顶点间在双向上都存在路径。
加权和未加权

解决的问题：比如搜索图中的一个特定顶点或搜索一条特定边，寻找图中的一条路径（从一个顶点到另一个顶点），寻找两个顶点之间的最短路径，以及环检测。

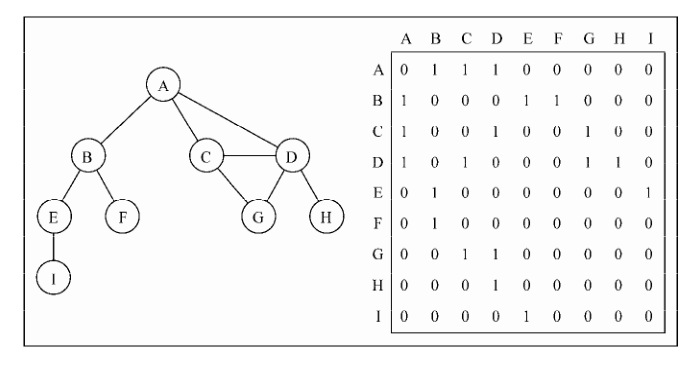
9.2 图的表示

9.2.1 邻接矩阵

如果索引为 i 的节点和索引为 j 的节点相邻，则 array[i][j]=== 1，否则 array[i][j] === 0

缺点： 1.不是强连通的图（稀疏图）如果用邻接矩阵来表示，则矩阵中将会有很多 0，这意味着我们浪费了计算机存储空间来表示根本不存在的边。 2.图中顶点的数量可能会改变，而 2 维数组不太灵活。

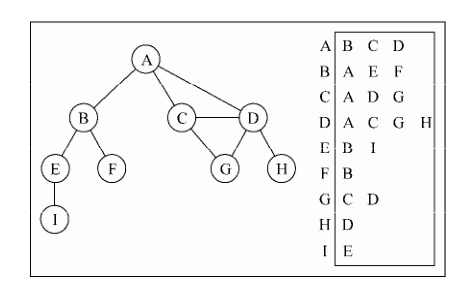
9.2.2 邻接表

可以用列表（数组）、链表，甚至是散列表或是字典来表示相邻顶点列表。（表第一行里的 BCD）

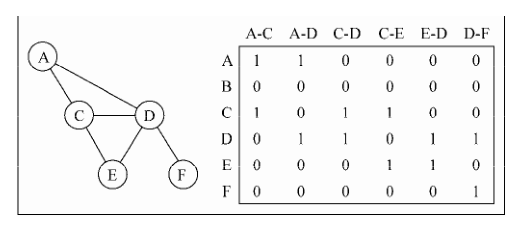
优缺点：尽管邻接表可能对大多数问题来说都是更好的选择，但以上两种表示法都很有用，且它们有着不同的性质（例如，要找出顶点 v 和 w 是否相邻，使用邻接矩阵会比较快）。

9.2.3 关联矩阵

如果顶点 v 是边 e 的入射点，则 array[v][e] === 1；否则，array[v][e] === 0。

解决的问题：关联矩阵通常用于边的数量比顶点多的情况下，以节省空间和内存。

9.3 创建图类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
function Graph() {

    var vertices = []; //list

    var adjList = new Dictionary();

    this.addVertex = function(v){
        vertices.push(v);
        adjList.set(v, []); //initialize adjacency list with array as well;
    };

    this.addEdge = function(v, w){
        adjList.get(v).push(w);
        //adjList.get(w).push(v); //commented to run the improved DFS with topological sorting
    };

    this.toString = function(){
        var s = '';
        for (var i=0; i<vertices.length; i++){
            s += vertices[i] + ' -> ';
            var neighbors = adjList.get(vertices[i]);
            for (var j=0; j<neighbors.length; j++){
                s += neighbors[j] + ' ';
            }
            s += '\n';
        }
        return s;
    };

    var initializeColor = function(){
        var color = [];
        for (var i=0; i<vertices.length; i++){
            color[vertices[i]] = 'white';
        }
        return color;
    };

    this.bfs = function(v, callback){

        var color = initializeColor(),
            queue = new Queue();
        queue.enqueue(v);

        while (!queue.isEmpty()){
            var u = queue.dequeue(),
                neighbors = adjList.get(u);
            color[u] = 'grey';
            for (var i=0; i<neighbors.length; i++){
                var w = neighbors[i];
                if (color[w] === 'white'){
                    color[w] = 'grey';
                    queue.enqueue(w);
                }
            }
            color[u] = 'black';
            if (callback) {
                callback(u);
            }
        }
    };

    this.dfs = function(callback){

        var color = initializeColor();

        for (var i=0; i<vertices.length; i++){
            if (color[vertices[i]] === 'white'){
                dfsVisit(vertices[i], color, callback);
            }
        }
    };

    var dfsVisit = function(u, color, callback){

        color[u] = 'grey';
        if (callback) {
            callback(u);
        }
        console.log('Discovered ' + u);
        var neighbors = adjList.get(u);
        for (var i=0; i<neighbors.length; i++){
            var w = neighbors[i];
            if (color[w] === 'white'){
                dfsVisit(w, color, callback);
            }
        }
        color[u] = 'black';
        console.log('explored ' + u);
    };


    this.BFS = function(v){

        var color = initializeColor(),
            queue = new Queue(),
            d = [],
            pred = [];
        queue.enqueue(v);

        for (var i=0; i<vertices.length; i++){
            d[vertices[i]] = 0;
            pred[vertices[i]] = null;
        }

        while (!queue.isEmpty()){
            var u = queue.dequeue(),
                neighbors = adjList.get(u);
            color[u] = 'grey';
            for (i=0; i<neighbors.length; i++){
                var w = neighbors[i];
                if (color[w] === 'white'){
                    color[w] = 'grey';
                    d[w] = d[u] + 1;
                    pred[w] = u;
                    queue.enqueue(w);
                }
            }
            color[u] = 'black';
        }

        return {
            distances: d,
            predecessors: pred
        };
    };

    var time = 0;
    this.DFS = function(){

        var color = initializeColor(),
            d = [],
            f = [],
            p = [];
        time = 0;

        for (var i=0; i<vertices.length; i++){
            f[vertices[i]] = 0;
            d[vertices[i]] = 0;
            p[vertices[i]] = null;
        }

        for (i=0; i<vertices.length; i++){
            if (color[vertices[i]] === 'white'){
                DFSVisit(vertices[i], color, d, f, p);
            }
        }

        return {
            discovery: d,
            finished: f,
            predecessors: p
        };
    };

    var DFSVisit = function(u, color, d, f, p){

        console.log('discovered ' + u);
        color[u] = 'grey';
        d[u] = ++time;
        var neighbors = adjList.get(u);
        for (var i=0; i<neighbors.length; i++){
            var w = neighbors[i];
            if (color[w] === 'white'){
                p[w] = u;
                DFSVisit(w,color, d, f, p);
            }
        }
        color[u] = 'black';
        f[u] = ++time;
        console.log('explored ' + u);
    };
}

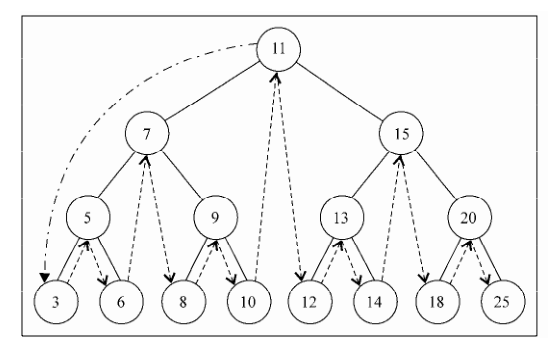
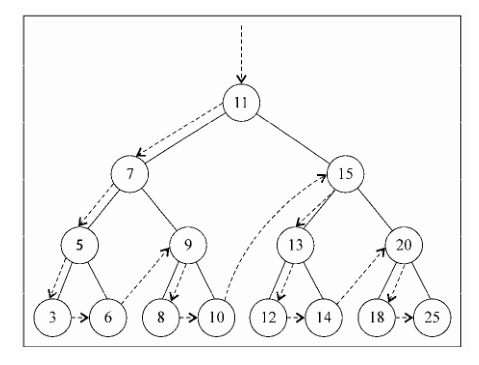
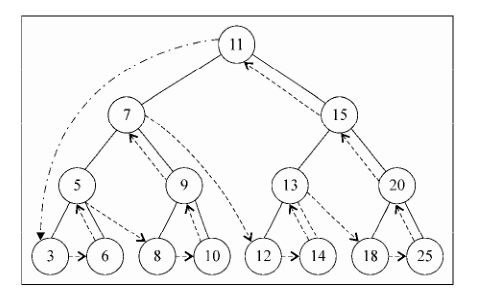
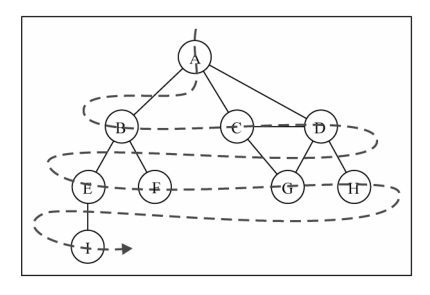
9.4 图的遍历

分为广度优先搜索（BFS）和深度优先搜索（DFS）
主要解决：最短路径问题及其变种问题

9.4.1 广度优先搜索

数据结构—栈

步骤：
(1) 创建一个队列 Q。
(2) 将 v 标注为被发现的（灰色），并将 v 入队列 Q。
(3) 如果 Q 非空，则运行以下步骤：
(a) 将 u 从 Q 中出队列；
(b) 将标注 u 为被发现的（灰色）；
(c) 将 u 所有未被访问过的邻点（白色）入队列；
(d) 将 u 标注为已被探索的（黑色）。

9.4.1.1 使用 BFS 寻找最短路径–从一个点到另外其他点所需要的路径

只是给原式添加两个参数：

9.4.1.2 深入学习最短路径

本章中的图不是加权图。如果要计算加权图中的最短路径（例如，城市 A 和城市 B 之间的最
短路径——GPS 和 Google Maps 中用到的算法），广度优先搜索未必合适。
举些例子，Dijkstra’s 算法解决了单源最短路径问题。Bellman–Ford 算法解决了边权值为负的
单源最短路径问题。A*搜索算法解决了求仅一对顶点间的最短路径问题，它用经验法则来加速搜索过程。Floyd–Warshall 算法解决了求所有顶点对间的最短路径这一问题。

9.4.2 深度优先搜索

数据结构—队列

9.4.2.1 探索深度优先算法

9.4.2.2 拓扑排序-使用深度优先搜索

10. 排序和搜索算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
function ArrayList(){

    var array = [];

    this.insert = function(item){
        array.push(item);
    };

    var swap = function(index1, index2){
        var aux = array[index1];
        array[index1] = array[index2];
        array[index2] = aux;
    };

    this.toString= function(){
        return array.join();
    };
//冒泡排序
    this.bubbleSort = function(){
        var length = array.length;

        for (var i=0; i<length; i++){
            console.log('--- ');
            for (var j=0; j<length-1; j++ ){
                console.log('compare ' + array[j] + ' with ' + array[j+1]);
                if (array[j] > array[j+1]){
                    console.log('swap ' + array[j] + ' with ' + array[j+1]);
                    swap(j, j+1);
                }
            }
        }
    };
//改进后的冒泡算法
    this.modifiedBubbleSort = function(){
        var length = array.length;

        for (var i=0; i<length; i++){
            console.log('--- ');
            for (var j=0; j<length-1-i; j++ ){          //改了这里--已经比较后，放在最后的就不需要再比较一次了
                console.log('compare ' + array[j] + ' with ' + array[j+1]);
                if (array[j] > array[j+1]){
                    console.log('swap ' + array[j] + ' with ' + array[j+1]);
                    swap(j, j+1);
                }
            }
        }

    };
//选择排序  --选择排序大致的思路是找到数据结构中的最小值并将其放置在第一位，接着找到第二小的值并将其放在第二位，以此类推。
    this.selectionSort = function(){
        var length = array.length,
            indexMin;

        for (var i=0; i<length-1; i++){
            indexMin = i;
            console.log('index ' + array[i]);
            for (var j=i; j<length; j++){
                if(array[indexMin]>array[j]){
                    console.log('new index min ' + array[j]);
                    indexMin = j;
                }
            }
            if (i !== indexMin){
                console.log('swap ' + array[i] + ' with ' + array[indexMin]);
                swap(i, indexMin);
            }
        }
    };
//插入排序 --插入排序每次排一个数组项，以此方式构建最后的排序数组。假定第一项已经排序了，接着，它和第二项进行比较，第二项是应该待在原位还是插到第一项之前呢？这样，头两项就已正确排序，接着和第三项比较（它是该插入到第一、第二还是第三的位置呢？），以此类推。
    this.insertionSort = function(){
        var length = array.length,
            j, temp;
        for (var i=1; i<length; i++){
            j = i;
            temp = array[i];
            console.log('to be inserted ' + temp);
            while (j>0 && array[j-1] > temp){
                console.log('shift ' + array[j-1]);
                array[j] = array[j-1];
                j--;
            }
            console.log('insert ' + temp);
            array[j] = temp;
        }
    };
//归并排序 --归并排序是第一个可以被实际使用的排序算法。你在本书中学到的前三个排序算法性能不好，但归并排序性能不错，其复杂度为O(nlog n )。
//归并排序是一种分治算法。其思想是将原始数组切分成较小的数组，直到每个小数组只有一个位置，接着将小数组归并成较大的数组，直到最后只有一个排序完毕的大数组。
    this.mergeSort = function(){
        array = mergeSortRec(array);
    };

    var mergeSortRec = function(array){

        var length = array.length;

        if(length === 1) {
            console.log(array);
            return array;
        }

        var mid = Math.floor(length / 2),
            left = array.slice(0, mid),
            right = array.slice(mid, length);

        return merge(mergeSortRec(left), mergeSortRec(right));
    };

    var merge = function(left, right){
        var result = [],
            il = 0,
            ir = 0;

        while(il < left.length && ir < right.length) {

            if(left[il] < right[ir]) {
                result.push(left[il++]);
            } else{
                result.push(right[ir++]);
            }
        }

        while (il < left.length){
            result.push(left[il++]);
        }

        while (ir < right.length){
            result.push(right[ir++]);
        }

        console.log(result);

        return result;
    };
//快速排序 --快速排序也许是最常用的排序算法了。它的复杂度为O(nlog n )，且它的性能通常比其他的复杂度为O(nlog n )的排序算法要好。
//和归并排序一样，快速排序也使用分治的方法，将原始数组分为较小的数组（但它没有像归并排序那样将它们分割开）。
    this.quickSort = function(){
        quick(array,  0, array.length - 1);
    };

    var partition = function(array, left, right) {

        var pivot = array[Math.floor((right + left) / 2)],
            i = left,
            j = right;

        console.log('pivot is ' + pivot + '; left is ' + left + '; right is ' + right);

        while (i <= j) {
            while (array[i] < pivot) {
                i++;
                console.log('i = ' + i);
            }

            while (array[j] > pivot) {
                j--;
                console.log('j = ' + j);
            }

            if (i <= j) {
                console.log('swap ' + array[i] + ' with ' + array[j]);
                swapQuickStort(array, i, j);
                i++;
                j--;
            }
        }

        return i;
    };

    var swapQuickStort = function(array, index1, index2){
        var aux = array[index1];
        array[index1] = array[index2];
        array[index2] = aux;
    };

    var quick = function(array, left, right){

        var index;

        if (array.length > 1) {

            index = partition(array, left, right);

            if (left < index - 1) {
                quick(array, left, index - 1);
            }

            if (index < right) {
                quick(array, index, right);
            }
        }
        return array;
    };
//顺序搜索  --就是判断相等
    this.sequentialSearch = function(item){

        for (var i=0; i<array.length; i++){
            if (item === array[i]){
                return i;
            }
        }

        return -1;
    };

    this.findMaxValue = function(){
        var max = array[0];
        for (var i=1; i<array.length; i++){
            if (max < array[i]){
                max = array[i];
            }
        }

        return max;
    };

    this.findMinValue = function(){
        var min = array[0];
        for (var i=1; i<array.length; i++){
            if (min > array[i]){
                min = array[i];
            }
        }

        return min;
    };
//二分搜索 --不大于不小于则一定相等
    this.binarySearch = function(item){
        this.quickSort();

        var low = 0,
            high = array.length - 1,
            mid, element;

        while (low <= high){
            mid = Math.floor((low + high) / 2);
            element = array[mid];
            console.log('mid element is ' + element);
            if (element < item) {
                low = mid + 1;
                console.log('low is ' + low);
            } else if (element > item) {
                high = mid - 1;
                console.log('high is ' + high);
            } else {
                console.log('found it');
                return mid;
            }
        }
        return -1;
    };

}

11. 算法补充知识

11.1 递归

一定要有边界条件
是跳转指令而不是子程序调用
溢出可以通过：时间和次数控制何时溢出错误

11.1.2 斐波那契数列

定义：
 1 和 2 的斐波那契数是 1；
 n（n>2）的斐波那契数是(n1)的斐波那契数加上(n2)的斐波那契数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//递归
function fibonacci(num){
    if (num === 1 || num === 2){
        return 1;
    }
    if (num > 2){
        return fibonacci(num - 1) + fibonacci(num - 2);
    }
}

//循环
function fib(num){
    var n1 = 1,
        n2 = 1,
        n = 1;
    for (var i = 3; i<=num; i++){
        n = n1 + n2;
        n1 = n2;
        n2 = n;
    }
    return n;
}

console.log(fibonacci(6));
console.log(fib(6));

ES6 用了尾调用优化，所以递归并不会更慢

11.2 动态规划

比较难-没搞懂

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
function MinCoinChange(coins){

    var coins = coins;

    var cache = {};

    this.makeChange = function(amount) {
        var me = this;
        if (!amount) {
            return [];
        }
        if (cache[amount]) {
            return cache[amount];
        }
        var min = [], newMin, newAmount;
        for (var i=0; i<coins.length; i++){
            var coin = coins[i];
            newAmount = amount - coin;
            if (newAmount >= 0){
                newMin = me.makeChange(newAmount);
            }
            if (
                newAmount >= 0 &&
                (newMin.length < min.length || !min.length) &&
                (newMin.length || !newAmount)
                ){
                min = [coin].concat(newMin);
                console.log('new Min ' + min + ' for ' + amount);
            }
        }
        return (cache[amount] = min);
    };
}

var minCoinChange = new MinCoinChange([1, 5, 16, 28]);
console.log(minCoinChange.makeChange(32));

11.3 贪心算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
function MinCoinChange(coins){

    var coins = coins;

    var cache = {};

    this.makeChange = function(amount) {
        var change = [],
            total = 0;
        for (var i=coins.length; i>=0; i--){
            var coin = coins[i];
            while (total + coin <= amount) {
                change.push(coin);
                total += coin;
            }
        }
        return change;
    };
}


var minCoinChange = new MinCoinChange([1, 5, 10, 25]);
console.log(minCoinChange.makeChange(36));

var minCoinChange2 = new MinCoinChange([1, 3, 4]);
console.log(minCoinChange2.makeChange(6));

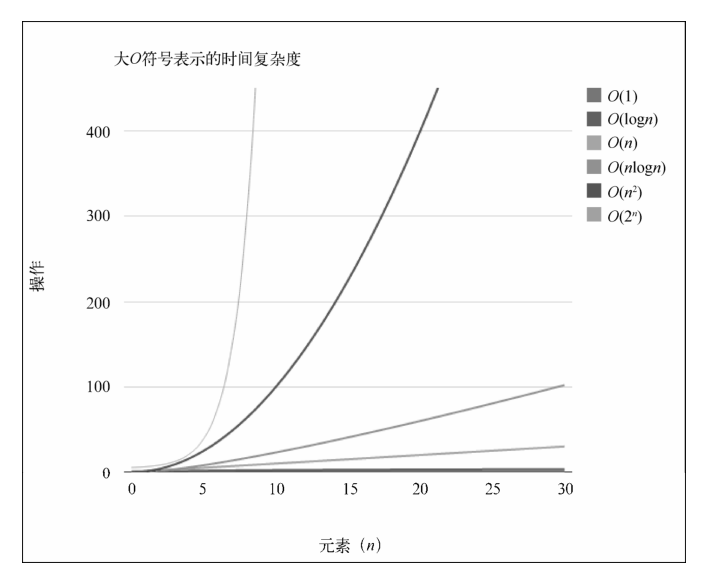
11.4 大 O 表示法

11.4.1 理解大 O 表示法

当讨论大 O 表示法时，一般考虑的是 CPU（时间）占用。

11.4.2 时间复杂度的比较

遇到的类算法公式

计算两个数字之间最大的公共除数（gcd）

harmony
1
2
const gcd = (x, y) => (!y ? x : gcd(y, x % y));
// gcd (8, 36) -> 4

解读：
先是把 x 当被除数，→ x%y，有余数说明不是整数倍
然后获取到余数
其实就是相当于找到余数的公共除数
所以余数再求他们的余数
y 提前的目的，是要交替相除，保证两个都能被除，而不是最后只有一边被除完

斐波那契数列

// 递归特别慢，采用循环

1
2
3
4
5
6
7
8
9
10
function fib(n) {
  let array = new Array(n + 1).fill(null);
  array[0] = 0;
  array[1] = 1;
  for (let i = 2; i <= n; i++) {
    array[i] = array[i - 1] + array[i - 2];
  }
  return array[n];
}
fib(10);

排序

冒泡算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 冒泡
function checkArray(array) {
  if (!array) return;
}
function swap(array, left, right) {
  let rightValue = array[right];
  array[right] = array[left];
  array[left] = rightValue;
}
function bubble(array) {
  checkArray(array);
  for (let i = array.length - 1; i > 0; i--) {
    // 从 0 到 `length - 1` 遍历
    for (let j = 0; j < i; j++) {
      if (array[j] > array[j + 1]) swap(array, j, j + 1);
    }
  }
  return array;
}

快排

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
var quickSort = function(arr) {
  if (arr.length <= 1) {
    return arr;
  }
  var pivotIndex = Math.floor(arr.length / 2);
  var pivot = arr.splice(pivotIndex, 1)[0];
  var left = [];
  var right = [];
  for (var i = 0; i < arr.length; i++) {
    if (arr[i] < pivot) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }
  return quickSort(left).concat([pivot], quickSort(right));
};

归并排序

核心代码部分：利用双指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
function Merger(a, b){
    var n = a && a.length;
    var m = b && b.length;
    var c = [];
     var i = 0, j = 0;

    while (i < n && j < m)  // 双指针
     {
         if (a[i] < b[j])
             c.push(a[i]);
             i++
         else
             c.push(b[j]);
             j++
     }

     while (i < n)
         c.push(a[i]);
         i++

     while (j < m)
         c.push(b[j]);
         j++

    console.log("将数组",a,'和',b,'合并为',c)
    return c;
}

动态规划总结

动态规划笔试题

子序列和子串

例如：一个字符串 awbcdewgh
他的子串： awbc. awbcd awbcde ….很多个子串 但是都是连续在一起
他的子序列： abc . abcd abcde … 很多个子序列 但是子序列中的字符在字符串中不一定是连在一起的， 但是 子序列一定是单调的

遍历二维数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 方法一：
var d_arr = new Array();
for (let i = 0; i < 4; i++) {
  d_arr[i] = new Array();
  for (let j = 0; j < 4; j++) {
    d_arr[i][j] = 0;
  }
}
console.log(d_arr);

// 方法二：
let arr = new Array(5).fill(0).map((v, index) => {
  return new Array(7).fill(0);
});

// 注意-下边这种方法是有问题的  里边生成的数组都是引用的一个数组，修改一个会都变
arr = new Array(5).fill(new Array(7));

最长公共子序列




1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
function LCS(str1, str2) {
  var m = str1.length;
  var n = str2.length;
  var dp = [new Array(n + 1).fill(0)]; //第一行全是0  初始化为0只是为了方便计算+1
  for (var i = 1; i <= m; i++) {
    //一共有m+1行
    dp[i] = [0]; //第一列全是[0] 数组☆ 会往这个数组里插入别的值，开始是0
    for (var j = 1; j <= n; j++) {
      //一共有n+1列
      if (str1[i - 1] === str2[j - 1]) {
        //注意这里，str1的第一个字符是在第二列中，因此要减1，str2同理
        dp[i][j] = dp[i - 1][j - 1] + 1; //对角＋1
      } else {
        dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
      }
    }
  }
  return dp[m][n];
}

// 自己写的，好理解
let s1 = [3, 4, 5, 6, 7, 8, 9, 0];
let s2 = [1, 2, 4, 6, 3, 7, 9];
function LCS(s1, s2) {
  var sl1 = s1.length;
  var sl2 = s2.length;
  var dp = new Array(sl1 + 1).fill(0).map(item => {
    return new Array(sl2 + 1).fill(0);
  }); // 记得长度要+1， 主要是为了下边运算-1的时候为-1
  for (var i = 1; i <= sl1; i++) {
    // 从1开始， 避免下边-1的时候为-1
    for (var j = 1; j <= sl2; j++) {
      if (s1[i - 1] === s2[j - 1]) {
        dp[i][j] = dp[i - 1][j - 1] + 1;
      } else {
        dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
      }
    }
  }
  console.log(dp, "dp");
}
// 自己写的2
let arr1 = ["B", "D", "C", "A", "B", "A"];
let arr2 = ["A", "B", "C", "B", "D", "A", "B"];

function Fun(s1, s2) {
  let twoArray = new Array(s1.length + 1).fill(0).map(item => {
    return new Array(s2.length + 1).fill(0);
  });
  twoArray[0][0] = 0;
  for (let index = 0; index < s1.length; index++) {
    twoArray[index][0] = 0;
    for (let index2 = 0; index2 < s2.length; index2++) {
      twoArray[0][index2] = 0;
      if (s1[index] === s2[index2]) {
        twoArray[index + 1][index2 + 1] = twoArray[index][index2] + 1;
        console.log(printFun(twoArray, s1, s2, index + 1, index2 + 1));
      } else {
        twoArray[index + 1][index2 + 1] = Math.max(
          twoArray[index][index2 + 1],
          twoArray[index + 1][index2]
        );
      }
    }
  }
  console.log(twoArray);
}
function printFun(twoArray, s1, s2, index, index2) {
  if (index == 0 || index2 == 0) {
    return "";
  }
  // 找下一个相同值， 先判断下一个s1s2值是否相同 -递归向上找
  if (s1[index - 1] === s2[index2 - 1]) {
    return printFun(twoArray, s1, s2, index - 1, index2 - 1) + s1[index - 1];
  }
  if (twoArray[index][index2 - 1] > twoArray[index - 1][index2]) {
    return printFun(twoArray, s1, s2, index, index2 - 1);
  } else {
    return printFun(twoArray, s1, s2, index - 1, index2);
  }
}
Fun(arr1, arr2);

参考文献

最长递增子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
function lis(n) {
  if (n.length === 0) return 0;
  // 创建一个和参数相同大小的数组，并填充值为 1 1的意思是最长子序列的长度为1个，每次都加1，是说明子序列的长度为+1
  let array = new Array(n.length).fill(1);
  // 从索引 1 开始遍历，因为数组已经所有都填充为 1 了
  for (let i = 1; i < n.length; i++) {
    // 从索引 0 遍历到 i
    // 判断索引 i 上的值是否大于之前的值
    for (let j = 0; j < i; j++) {
      if (n[i] > n[j]) {
        array[i] = Math.max(array[i], 1 + array[j]);
      }
    }
  }
  console.log(array);
  let res = 1;
  for (let i = 0; i < array.length; i++) {
    res = Math.max(res, array[i]);
  }
  return res;
}
lis([3, 5, 2, 6, 9, 1, 3, 4]); // 4
// [1, 2, 1, 3, 4, 1, 2, 3]

// 自己写的
var s1 = [3, 5, 2, 6, 9, 1, 3, 4];
// var s1 = [6,4,3,4,5,8,7,2]
function fun(s1) {
  var countArr = new Array(s1.length).fill(1); // 从1开始
  for (var i = 1; i < s1.length; i++) {
    for (var j = 0; j < i; j++) {
      if (s1[i] > s1[j]) {
        countArr[i] = Math.max(countArr[i], 1 + countArr[j]); // 因为多次循环不同的j， countArr[i]多次赋值，取最大的一次
      }
    }
  }
  console.log(countArr);
}

fun(s1);
// [ 0, 1, 2, 3, 2, 3, 1, 0 ] 'countArr'

方法二：
公共子序列法

1
2
[3, 5, 2, 6, 9, 1, 3, 4].sort(); // [1, 2, 3, 3, 4, 5, 6, 9]
//求 [1, 2, 3, 3, 4, 5, 6, 9]  和 [3,5,2,6,9,1,3,4] 的公共子序列

01 背包问题

用途：价值总和最大



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
function knapsack(weights, values, W) {
  var n = weights.length - 1;
  var f = [[]];
  for (var j = 0; j <= W; j++) {
    if (j < weights[0]) {
      //如果容量不能放下物品0的重量，那么价值为0
      f[0][j] = 0;
    } else {
      //否则等于物体0的价值
      f[0][j] = values[0];
    }
  }
  for (var j = 0; j <= W; j++) {
    for (var i = 1; i <= n; i++) {
      if (!f[i]) {
        //创建新一行
        f[i] = [];
      }
      if (j < weights[i]) {
        //等于之前的最优值
        f[i][j] = f[i - 1][j];
      } else {
        f[i][j] = Math.max(f[i - 1][j], f[i - 1][j - weights[i]] + values[i]);
      }
    }
  }
  return f[n][W];
}
var a = knapsack([2, 2, 6, 5, 4], [6, 3, 5, 4, 6], 10);
console.log(a);

// 自己写的
let weight = [2, 2, 6, 5, 4];
let values = [6, 3, 5, 4, 6];
let W = 10;
function fun(weight, values, W) {
  let TDA = new Array(W + 1).fill(0).map(item => {
    return new Array(weight.length).fill(0);
  });
  for (var i = 0; i <= W; i++) {
    for (let j = 0; j < weight.length; j++) {
      if (i >= weight[j]) {
        if (j > 0) {
          // 不是第一行的时候，因为第一行在下边不能j-1
          //放
          let push = values[j] + TDA[i - weight[j]][j - 1];
          // 不放-取上一个值
          let noPush = TDA[i][j - 1];
          TDA[i][j] = Math.max(push, noPush);
        } else {
          TDA[i][j] = values[0];
        }
      } else {
        // 不放入-取上一个值
        if (j > 0) {
          TDA[i][j] = TDA[i][j - 1];
        } else {
          TDA[i][j] = 0;
        }
      }
    }
  }
  console.log(TDA);
}
fun(weight, values, W);
// 代码总结copy
/**
 * @param {*} w 物品重量
 * @param {*} v 物品价值
 * @param {*} C 总容量
 * @returns
 */
function knapsack(w, v, C) {
  let length = w.length;
  if (length === 0) return 0;

  // 对照表格，生成的二维数组，第一维代表物品，第二维代表背包剩余容量
  // 第二维中的元素代表背包物品总价值
  let array = new Array(length).fill(new Array(C + 1).fill(null));

  // 完成底部子问题的解
  for (let i = 0; i <= C; i++) {
    // 对照表格第一行， array[0] 代表物品 1
    // i 代表剩余总容量
    // 当剩余总容量大于物品 1 的重量时，记录下背包物品总价值，否则价值为 0
    array[0][i] = i >= w[0] ? v[0] : 0;
  }

  // 自底向上开始解决子问题，从物品 2 开始
  for (let i = 1; i < length; i++) {
    for (let j = 0; j <= C; j++) {
      // 这里求解子问题，分别为不放当前物品和放当前物品
      // 先求不放当前物品的背包总价值，这里的值也就是对应表格中上一行对应的值
      array[i][j] = array[i - 1][j];
      // 判断当前剩余容量是否可以放入当前物品
      if (j >= w[i]) {
        // 可以放入的话，就比大小
        // 放入当前物品和不放入当前物品，哪个背包总价值大
        array[i][j] = Math.max(array[i][j], v[i] + array[i - 1][j - w[i]]);
      }
    }
  }
  return array[length - 1][C];
}
// 自己写的硬币问题
var money = [1, 2, 5, 10, 20, 50, 100];

function fun(n) {
  let arr = new Array(n + 1).fill(0).map(item => {
    return new Array(money.length).fill(0);
  });
  for (var i = 0; i < n; i++) {
    if (i < money[0]) {
      arr[i][0] = 0;
    } else {
      arr[i][0] = 1;
    }
  }
  for (var i = 0; i <= n; i++) {
    for (var j = 1; j < money.length; j++) {
      if (i >= money[j]) {
        // 注意要等于
        arr[i][j] = Math.max(
          arr[i][j - 1],
          arr[i - money[j]][j - 1] + money[j]
        );
        // 如果是完全背包
        // arr[i][j] = Math.max(arr[i][j-1], arr[i-money[j]][j] + money[j])  // 只是稍微修改了这里
        // 如果说是多少种放法
        // arr[i][j] = arr[i-money[j]][j-1] + arr[i][j]
      } else {
        arr[i][j] = arr[i][j - 1];
      }
    }
  }
  console.log(arr[100], "100");
}
fun(110);

// 完全背包-硬币
// 先看普通背包
for (var i = 0; i < n; i++) {
  for (var j = 0; j <= W; j++) {
    f[i][j] = Math.max(f[i - 1][j], f[i - 1][j - weights[i]] + values[i]);
  }
}
// 完全背包-方法一:再次遍历k
for (var i = 0; i < n; i++) {
  for (var j = 0; j <= W; j++) {
    for (var k = 0; k < j / weights[i]; k++) {
      f[i][j] = Math.max(
        f[i - 1][j],
        f[i - 1][j - k * weights[i]] + k * values[i]
      );
    }
  }
}
// 完全背包-方法二:f[i-1]变为f[i]
for (let i = 0; i < n; i++) {
  f[i] = [];
  for (let j = 0; j <= W; j++) {
    if (j < weights[i]) {
      f[i][j] = f[i - 1][j];
    } else {
      f[i][j] = Math.max(f[i - 1][j], f[i][j - weights[i]] + values[i]);
    }
  }
}

参考文献
动态规划

树结构

树的数据结构

1
2
3
4
5
6
7
8
9
10
11
12
13
let a = {
    value: '1'
    left: {
        value: '2',
        left:{},
        right:{}
    },
    right:{
        value: '3',
        left:{},
        right:{}
    }
}

树的添加，查找和删除节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
// 自己写的
class Node {
  constructor(data, left, right) {
    this.data = data;
    this.left = left;
    this.right = right;
  }
}

class Tree {
  constructor() {
    this.root = null;
    this.deepDataList = [];
    this.breadthDataList = [];
    this.breadthNodeList = [];
    this.breadthCount = 0;
  }
  // 形成排序二叉树
  insert(data) {
    let newNode = new Node(data, null, null);
    if (!this.root) {
      return (this.root = newNode);
    }
    let currentNode = this.root;
    // let parentNode = null;
    while (1) {
      if (data < currentNode.data) {
        if (currentNode.left) {
          currentNode = currentNode.left;
        } else {
          currentNode.left = newNode;
          break;
        }
      } else {
        if (currentNode.right) {
          currentNode = currentNode.right;
        } else {
          currentNode.right = newNode;
          break;
        }
      }
    }
  }
  // 先序遍历 先访问根节点，然后访问左节点，最后访问右节点 - 复制一个排序二叉树最快 / 显示目录结构
  preTraversal(node) {
    if (!node) return;
    console.log(node.data, "pre");
    this.preTraversal(node.left);
    this.preTraversal(node.right);
  }
  // 中序遍历 先访问左节点，然后访问根节点，最后访问右节点 - 用于排序   /  实现表达式树，在编译器底层很有用
  midTraversal(node) {
    if (!node) return;
    this.midTraversal(node.left);
    console.log(node.data, "mid");
    this.midTraversal(node.right);
  }
  // 后序遍历 先访问左节点，然后访问右节点，最后访问根节点 - 文件系统常用 / 计算目录内的文件及其信息
  backTraversal(node) {
    if (!node) return;
    this.backTraversal(node.left);
    this.backTraversal(node.right);
    console.log(node.data, "back");
  }
  // https://www.jianshu.com/p/b4d8085e84bd
  // https://www.jianshu.com/p/5e9ea25a1aae
  // 深度优先-上边的所有（先序、中序、后序）都是深度优先！ 沿着一条路径一直找到最深的那个节点，当没有子节点的时候，返回上一级节点，寻找其另外的子节点，继续向下遍历，没有就向上返回一级，直到所有的节点都被遍历到，每个节点只能访问一次。
  // 6 4 3 5 8 7 9
  deepTraversal(node) {
    if (node) {
      this.deepDataList.push(node.data); // 这个其实就是先序遍历
      this.deepTraversal(node.left);
      this.deepTraversal(node.right);
    }
  }

  // 广度优先 - 之字遍历  一层之后下一层
  // 6 4 8 3 5 7 9
  breadthTraversal(root) {
    // 传入根节点
    if (root) {
      this.breadthNodeList[this.breadthCount] = root;
    }
    let node = this.breadthNodeList[this.breadthCount];
    if (node) {
      this.breadthDataList.push(node.data); // 这里改成console也可以
      this.breadthNodeList.push(node.left);
      this.breadthNodeList.push(node.right);
      this.breadthCount++;
      this.breadthTraversal();
    }
  }
  // 更优的写法
  var levelOrder = function(root) {
    if (!root) {
        return [];
    }

    const data = [];
    const queue = [root];
    while (queue.length) {
        const first = queue.shift();
        data.push(first.val);
        first.left && queue.push(first.left);
        first.right && queue.push(first.right);
    }
    return data;
};

  // 深度
  maxDepth(node) {
    if (!node) return 0;
    return Math.max(this.maxDepth(node.left), this.maxDepth(node.right)) + 1;
  }
  // 查找 - 直接用先序遍历就可以进行递归
  find(searchNode, node) {
    if (searchNode.data == node.data) {
      return node.data;
    }
    find(node.left);
    find(node.right);
  }
}
//    6
//  4   8
// 3 5 7 9

let tree = new Tree();
tree.insert(6);
tree.insert(4);
tree.insert(3);
tree.insert(5);
tree.insert(8);
tree.insert(7);
tree.insert(9);
// console.log(tree.root);
// tree.midTraversal(tree.root);
// tree.preTraversal(tree.root);
// tree.backTraversal(tree.root);
// tree.deepTraversal(tree.root);
// tree.breadthTraversal(tree.root);
console.log(tree.maxDepth(tree.root));

// 网上找的
class BinarySearchTree {
  constructor() {
    this.root = null;
  }
  insert(data) {
    let n = new Node(data, null, null);
    if (!this.root) {
      return (this.root = n);
    }
    let currentNode = this.root;
    let parent = null;
    while (1) {
      parent = currentNode;
      if (data < currentNode.data) {
        currentNode = currentNode.left;
        if (currentNode === null) {
          parent.left = n;
          break;
        }
      } else {
        currentNode = currentNode.right;
        if (currentNode === null) {
          parent.right = n;
          break;
        }
      }
    }
  }
  remove(data) {
    this.root = this.removeNode(this.root, data);
  }
  removeNode(node, data) {
    if (node == null) {
      return null;
    }
    if (data == node.data) {
      // no children node
      if (node.left == null && node.right == null) {
        return null;
      }
      if (node.left == null) {
        return node.right;
      }
      if (node.right == null) {
        return node.left;
      }
      let getSmallest = function(node) {
        if (node.left === null && node.right == null) {
          return node;
        }
        if (node.left != null) {
          return node.left;
        }
        if (node.right !== null) {
          return getSmallest(node.right);
        }
      };
      let temNode = getSmallest(node.right);
      node.data = temNode.data;
      node.right = this.removeNode(temNode.right, temNode.data);
      return node;
    } else if (data < node.data) {
      node.left = this.removeNode(node.left, data);
      return node;
    } else {
      node.right = this.removeNode(node.right, data);
      return node;
    }
  }
  find(data) {
    var current = this.root;
    while (current != null) {
      if (data == current.data) {
        break;
      }
      if (data < current.data) {
        current = current.left;
      } else {
        current = current.right;
      }
    }
    return current.data;
  }
}
module.exports = BinarySearchTree;

// 重建二叉树
var buildTree = function(preorder, inorder) {
    var result = null;
    if(preorder.length > 1){
        var index = inorder.indexOf(preorder[0]);
        result = {
            val: preorder[0],
            left: buildTree(preorder.slice(1, index + 1), inorder.slice(0, index)),
            right: buildTree(preorder.slice(index + 1), inorder.slice(index + 1))
        }
    }else if(preorder.length == 1){
        result = {
            val: preorder[0],
            left: null,
            right: null
        }
    }
    return result;
};
console.log(buildTree([3,9,20,15,7], [9,3,15,20,7]))

树的深度

1
2
3
4
var maxDepth = function(root) {
  if (!root) return 0;
  return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
};

二维数组的全排列组合

用途：一共有多少种方法

// 核心思想就是 从 0 开始， 一点一点+1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
function printArr(arr, n, res) {
  for (var i = 0; i < arr[i].length; i++) {
    if (n == 0) {
      res = [];
    }
    if (n < arr.length) {
      var _res = res.slice();
      _res.push(arr[n][i]);
      if (n == arr.length - 1) {
        console.log(_res);
      } else {
        printArr(arr, n + 1, _res);
      }
    }
  }
}
// 测试：
var arr = [
  [1, 2],
  [3, 4],
  [5, 6]
];
printArr(arr, 0);
// [ 1, 3, 5 ]
// [ 1, 3, 6 ]
// [ 1, 4, 5 ]
// [ 1, 4, 6 ]
// [ 2, 3, 5 ]
// [ 2, 3, 6 ]
// [ 2, 4, 5 ]
// [ 2, 4, 6 ]

// 自己写的方法二
var arr = [
  [1, 2],
  [3, 4],
  [5, 6]
];

function printArr(arr, n, res) {
  if (n == 0) res = [];
  var i = 0;
  while (i < arr[n].length) {
    var newRes = res.slice();
    newRes.push(arr[n][i]);
    if (n == arr.length - 1) {
      console.log(newRes);
    } else {
      var newN = n + 1;
      printArr(arr, newN, newRes);
    }
    i++;
  }
}
printArr(arr, 0);

打印青蛙跳台阶的所有方式

注意 不是求方式的个数，而是打印每种情况台阶数为 10，每次跳 1 次或两次

可以拆开为[[1,2],[1,2],[1,2]] 这样，控制总数为 10

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function step(n, res) {
  if (n == 0) {
    res = [];
  }
  var i = 1;
  while (i < 3) {
    if (n + i <= 10) {
      var _res = res.slice();
      _res.push(i);
      if (n + i == 10) {
        console.log(_res);
      } else {
        step(n + i, _res);
      }
    }
    i++;
  }
}
step(0);

变种： [10,20,50,100] 随便取最后得 1000

计算数位之和

例如：78 就是 7+8

1
2
3
4
5
6
7
8
function bitSum(n) {
  let res = 0;
  while (n) {
    res = res + (n % 10);
    n = Math.floor(n / 10);
  }
  return res;
}
← Prev Next →